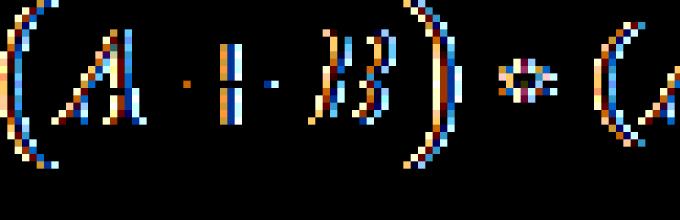Способы решения систем логических уравнений. Логика

Можно выделить различные способы решения систем логических уравнений. Это сведение к одному уравнению, построение таблицы истинности и декомпозиция.

Задача: Решить систему логических уравнений:

Рассмотрим метод сведения к одному уравнению . Данный метод предполагает преобразование логических уравнений, таким образом, чтобы правые их части были равны истинностному значению (то есть 1). Для этого применяют операцию логического отрицания. Затем, если в уравнениях есть сложные логические операции, заменяем их базовыми: «И», «ИЛИ», «НЕ». Следующим шагом объединяем уравнения в одно, равносильное системе, с помощью логической операции «И». После этого, следует сделать преобразования полученного уравнения на основе законов алгебры логики и получить конкретное решение системы.

Решение 1: Применяем инверсию к обеим частям первого уравнения:

Представим импликацию через базовые операции «ИЛИ», «НЕ»:

Поскольку левые части уравнений равны 1, можно объединить их с помощью операции “И” в одно уравнение, равносильное исходной системе:

Раскрываем первую скобку по закону де Моргана и преобразовываем полученный результат:

Полученное уравнение, имеет одно решение: A =0, B=0 и C=1.

Следующий способ – построение таблиц истинности . Поскольку логические величины имеют только два значения, можно просто перебрать все варианты и найти среди них те, при которых выполняется данная система уравнений. То есть, мы строим одну общую таблицу истинности для всех уравнений системы и находим строку с нужными значениями.

Решение 2: Составим таблицу истинности для системы:








0	0	1	1	0	1

Полужирным выделена строчка, для которой выполняются условия задачи. Таким образом, A=0, B=0 и C=1.

Способ декомпозиции . Идея состоит в том, чтобы зафиксировать значение одной из переменных (положить ее равной 0 или 1) и за счет этого упростить уравнения. Затем можно зафиксировать значение второй переменной и т.д.

Решение 3: Пусть A = 0, тогда:

Из первого уравнения получаем B =0, а из второго – С=1. Решение системы: A = 0, B = 0 и C = 1.

В ЕГЭ по информатике очень часто требуется определить количество решений системы логических уравнений, без нахождения самих решений, для этого тоже существуют определенные методы. Основной способ нахождения количества решений системы логических уравнений – замена переменных . Сначала необходимо максимально упростить каждое из уравнений на основе законов алгебры логики, а затем заменить сложные части уравнений новыми переменными и определить количество решений новой системы. Далее вернуться к замене и определить для нее количество решений.

Задача: Сколько решений имеет уравнение (A →B ) + (C →D ) = 1? Где A, B, C, D – логические переменные.

Решение: Введем новые переменные: X = A →B и Y = C →D . С учетом новых переменных уравнение запишется в виде: X + Y = 1.

Дизъюнкция верна в трех случаях: (0;1), (1;0) и (1;1), при этом X и Y является импликацией, то есть является истинной в трех случаях и ложной – в одном. Поэтому случай (0;1) будет соответствовать трем возможным сочетаниям параметров. Случай (1;1) – будет соответствовать девяти возможным сочетаниям параметров исходного уравнения. Значит, всего возможных решений данного уравнения 3+9=15.

Следующий способ определения количества решений системы логических уравнений – бинарное дерево . Рассмотрим данный метод на примере.

Задача: Сколько различных решений имеет система логических уравнений:

Приведенная система уравнений равносильна уравнению:

(x 1 → x 2 )*(x 2 → x 3 )*…*(x m -1 → x m ) = 1.

Предположим, что x 1 – истинно, тогда из первого уравнения получаем, что x 2 также истинно, из второго - x 3 =1, и так далее до x m = 1. Значит набор (1; 1; …; 1) из m единиц является решением системы. Пусть теперь x 1 =0, тогда из первого уравнения имеем x 2 =0 или x 2 =1.

Когда x 2 истинно получаем, что остальные переменные также истинны, то есть набор (0; 1; …; 1) является решением системы. При x 2 =0 получаем, что x 3 =0 или x 3 =, и так далее. Продолжая до последней переменной, получаем, что решениями уравнения являются следующие наборы переменных (m +1 решение, в каждом решении по m значений переменных):

(1; 1; 1; …; 1)

(0; 1; 1; …; 1)

(0; 0; 0; …; 0)

Такой подход хорошо иллюстрируется с помощью построения бинарного дерева. Количество возможных решений – количество различных ветвей построенного дерева. Легко заметить, что оно равно m +1.

	Дерево	Количество решений
x 1
x 2
x 3
		…

В случае трудностей в рассужд ниях и построении де рева решений можно искать решение с использованием таблиц истинности , для одного – двух уравнений.

Перепишем систему уравнений в виде:

И составим таблицу истинности отдельно для одного уравнения:

x 1	x 2	(x 1 → x 2)

Составим таблицу истинности для двух уравнений:

x 1	x 2	x 3	x 1 → x 2	x 2 → x 3	(x 1 → x 2) (x 2 → x 3)*

Назначение сервиса . Онлайн-калькулятор предназначен для построения таблицы истинности для логического выражения .
Таблица истинности – таблица содержащая все возможные комбинации входных переменных и соответствующее им значения на выходе.
Таблица истинности содержит 2 n строк, где n – число входных переменных, и n+m – столбцы, где m – выходные переменные.

Инструкция . При вводе с клавиатуры используйте следующие обозначения:

Например, логическое выражение abc+ab~c+a~bc необходимо ввести так: a*b*c+a*b=c+a=b*c
Для ввода данных в виде логической схемы используйте этот сервис .

Правила ввода логической функции

Вместо символа v (дизъюнкция, ИЛИ) используйте знак + .
Перед логической функцией не надо указывать обозначение функции. Например, вместо F(x,y)=(x|y)=(x^y) необходимо ввести просто (x|y)=(x^y) .
Максимальное количество переменных равно 10 .

Проектирование и анализ логических схем ЭВМ ведётся с помощью специального раздела математики - алгебры логики. В алгебре логики можно выделить три основные логические функции: "НЕ" (отрицание), "И" (конъюнкция), "ИЛИ" (дизъюнкция).
Для создания любого логического устройства необходимо определить зависимость каждой из выходных переменных от действующих входных переменных такая зависимость называется переключательной функцией или функцией алгебры логики.
Функция алгебры логики называется полностью определённой если заданы все 2 n её значения, где n – число выходных переменных.
Если определены не все значения, функция называется частично определённой.
Устройство называется логическим, если его состояние описывается с помощью функции алгебры логики.
Для представления функции алгебры логики используется следующие способы:
По алгебраической форме можно построить схему логического устройства, используя логические элементы.

Рисунок1- Схема логического устройства

Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможны х логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2 N строк, так как существует 2 N различных комбинаций возможных значений аргументов.

Операция НЕ - логическое отрицание (инверсия)

Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее:

если исходное выражение истинно, то результат его отрицания будет ложным;
если исходное выражение ложно, то результат его отрицания будет истинным.

Для операции отрицания НЕ приняты следующие условные обозначения:
не А, Ā, not A, ¬А, !A
Результат операции отрицания НЕ определяется следующей таблицей истинности:

A	не А
0	1
1	0

Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.

Операция ИЛИ - логическое сложение (дизъюнкция, объединение)

Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.
Применяемые обозначения: А или В, А V В, A or B, A||B.
Результат операции ИЛИ определяется следующей таблицей истинности:
Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В - ложны.

Операция И - логическое умножение (конъюнкция)

Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.
Применяемые обозначения: А и В, А Λ В, A & B, A and B.
Результат операции И определяется следующей таблицей истинности:

A	B	А и B
0	0	0
0	1	0
1	0	0
1	1	1

Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.

Операция «ЕСЛИ-ТО» - логическое следование (импликация)

Эта операция связывает два простых логических выражения, из которых первое является условием, а второе - следствием из этого условия.
Применяемые обозначения:
если А, то В; А влечет В; if A then В; А→ В.
Таблица истинности:

A	B	А → B
0	0	1
0	1	1
1	0	0
1	1	1

Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.

Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)

Применяемое обозначение: А ↔ В, А ~ В.
Таблица истинности:

A	B	А↔B
0	0	1
0	1	0
1	0	0
1	1	1

Операция «Сложение по модулю 2» (XOR, исключающее или, строгая дизъюнкция)

Применяемое обозначение: А XOR В, А ⊕ В.
Таблица истинности:

A	B	А⊕B
0	0	0
0	1	1
1	0	1
1	1	0

Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.

Приоритет логических операций

Действия в скобках
Инверсия
Конъюнкция (&)
Дизъюнкция (V), Исключающее ИЛИ (XOR), сумма по модулю 2
Импликация (→)
Эквивалентность (↔)

Совершенная дизъюнктивная нормальная форма

Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:

Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x 1 ,x 2 ,...x n).
Все логические слагаемые формулы различны.
Ни одно логическое слагаемое не содержит переменную и её отрицание.
Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.

СДНФ можно получить или с помощью таблиц истинности или с помощью равносильных преобразований.
Для каждой функции СДНФ и СКНФ определены единственным образом с точностью до перестановки.

Совершенная конъюнктивная нормальная форма

Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:

Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x 1 ,x 2 ,...x n).
Все элементарные дизъюнкции различны.
Каждая элементарная дизъюнкция содержит переменную один раз.
Ни одна элементарная дизъюнкция не содержит переменную и её отрицание.

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 18»

городского округа город Салават Республики Башкортостан

Системы логических уравнений

в задачах ЕГЭ по информатике

Раздел «Основы алгебры логики» в заданиях ЕГЭ считается одним из самых сложных и плохо решаемых. Средний процент выполнения заданий по данной теме самый низкий и составляет 43,2.

Раздел курса	Средний процент выполнения по группам заданий
Кодирование информации и измерение ее количества
Информационное моделирование
Системы счисления
Основы алгебры логики
Алгоритмизация и программирование
Основы информационно- коммуникационных технологий

Исходя из спецификации КИМа 2018 года этот блок включает четыре задания разного уровня сложности.

№ задания	Проверяемые элементы содержания	Уровень сложности задания
	Умение строить таблицы истинности и логические схемы
	Умение осуществлять поиск информации в сети Интернет
	Знание основных понятий и законов математической логики
	Умение строить и преобразовывать логические выражения

Задание 23 является высоким по уровню сложности, поэтому имеет самый низкий процент выполнения. Среди подготовленных выпускников (81-100 баллов) 49,8% выполнивших, средне подготовленные (61-80 баллов) справляются на 13,7%, оставшаяся группа учеников данное задание не выполняет.

Успешность решения системы логических уравнений зависит от знания законов логики и от четкого применения методов решения системы.

Рассмотрим решение системы логических уравнений методом отображения.

(23.154 Поляков К.Ю.) Сколько различных решений имеет система уравнений?

((x 1  y 1 )  (x 2  y 2 ))  (x 1  x 2 )  (y 1  y 2 ) =1

((x 2  y 2 )  (x 3  y 3 ))  (x 2  x 3 )  (y 2  y 3 ) =1

((x 7  y 7 )  (x 8  y 8 ))  (x 7  x 8 )  (y 7  y 8 ) =1

где x 1 , x 2 ,…, x 8, у 1 ,у 2 ,…,у 8 - логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Решение . Все уравнения, включенные в систему, однотипны, и в каждое уравнение включено четыре переменных. Зная x1 и y1, можем найти все возможные значения x2 и y2, удовлетворяющие первому уравнению. Рассуждая аналогичным образом, из известных x2 и y2можем найти x3, y3, удовлетворяющее второму уравнению. То есть, зная пару (x1 , y1) и определив значение пары (x2 , y2) , мы найдем пару (x3 , y3 ), которая, в свою очередь, приведет к паре (x4 , y4 ) и так далее.

Найдем все решения первого уравнения. Это можно сделать двумя способами: построить таблицу истинности, через рассуждения и применение законов логики.

Таблица истинности:

x 1  y 1	x 2  y 2	(x 1  y 1 )  (x 2  y 2 )	(x 1  x 2 )	(y 1  y 2 )	(x 1  x 2 )  (y 1  y 2 )

Построение таблицы истинности трудоемко и неэффективно по времени, поэтому применяем второй способ - логические рассуждения. Произведение равно 1 тогда и только тогда, когда каждый множитель равен 1.

(x 1  y 1 )  (x 2  y 2 ))=1

(x 1  x 2 ) =1

(y 1  y 2 ) =1

Рассмотрим первое уравнение. Следование равно 1, когда 0 0, 0 1, 1 1, значит (x1 y1)=0 при (01), (10), то пара (x 2  y 2 ) может быть любой (00), (01), (10), (11), а при (x1 y1)=1, то есть (00) и (11) пара (x2 y2)=1 принимает такие же значения (00) и (11). Исключим из этого решения те пары, для которых ложны второе и третье уравнения, то есть x1=1, x2=0, y1=1, y2=0.

(x 1 , y 1 )	(x 2 , y 2 )

Общее количество пар 1+1+1+22=25

2) (23.160 Поляков К.Ю.) Сколько различных решений имеет система логических уравнений

(x 1  (x 2  y 2 ))  (y 1  y 2 ) = 1

(x 2  (x 3  y 3 ))  (y 2  y 3 ) = 1

...

( x 6  ( x 7  y 7 ))  ( y 6  y 7 ) = 1

x 7  y 7 = 1

Решение. 1) Уравнения однотипные, поэтому методом рассуждения найдем всевозможные пары (x1,y1), (x2,y2) первого уравнения.

(x 1  (x 2  y 2 ))=1

(y 1  y 2 ) = 1

Решением второго уравнения являются пары (00), (01), (11).

Найдем решения первого уравнения. Если x1=0, то x2 , y2 - любые, если x1=1, то x2 , y2 принимает значение (11).

Составим связи между парами (x1 , y1) и (x2 , y2).

(x 1 , y 1 )	(x 2 , y 2 )

Составим таблицу для вычисления количества пар на каждом этапе.




							0

Учитывая решения последнего уравнения x 7  y 7 = 1, исключим пару (10). Находим общее число решений 1+7+0+34=42

3)(23.180) Сколько различных решений имеет система логических уравнений

(x 1  x 2 )  (x 3  x 4 ) = 1

(x 3  x 4 )  (x 5  x 6 ) = 1

(x 5  x 6 )  (x 7  x 8 ) = 1

(x 7  x 8 )  (x 9  x 10 ) = 1

x 1  x 3  x 5  x 7  x 9 = 1

Решение. 1) Уравнения однотипные, поэтому методом рассуждения найдем всевозможные пары (x1,x2), (x3,x4) первого уравнения.

(x 1  x 2 )  (x 3  x 4 ) = 1

Исключим из решения пары, которые в следовании дают 0 (1 0), это пары (01, 00, 11) и (10).

Составим связи между парами (x1,x2), (x3,x4)

Как решать некоторые задачи разделов A и B экзамена по информатике

Урок №3. Логика. Логические функции. Решение уравнений

Большое количество задач ЕГЭ посвящено логике высказываний. Для решения большинства из них достаточно знания основных законов логики высказываний, знания таблиц истинности логических функций одной и двух переменных. Приведу основные законы логики высказываний.

Коммутативность дизъюнкции и конъюнкции:
a ˅ b ≡ b ˅ a
a ^ b ≡ b ^ a
Дистрибутивный закон относительно дизъюнкции и конъюнкции:
a ˅ (b^с) ≡ (a ˅ b) ^(a ˅ с)
a ^ (b ˅ с) ≡ (a ^ b) ˅ (a ^ с)
Отрицание отрицания:
¬(¬а) ≡ а
Непротиворечивость:
a ^ ¬а ≡ false
Исключающее третье:
a ˅ ¬а ≡ true
Законы де-Моргана:
¬(а ˅ b) ≡ ¬а ˄ ¬b
¬(а ˄ b) ≡ ¬а ˅ ¬b
Упрощение:
a ˄ a ≡ a
a ˅ a ≡ a
a ˄ true ≡ a
a ˄ false ≡ false
Поглощение:
a ˄ (a ˅ b) ≡ a
a ˅ (a ˄ b) ≡ a
Замена импликации
a → b ≡ ¬a ˅ b
Замена тождества
a ≡ b ≡(a ˄ b) ˅ (¬a ˄ ¬b)

Представление логических функций

Любую логическую функцию от n переменных – F(x 1 , x 2 , … x n) можно задать таблицей истинности. Такая таблица содержит 2 n наборов переменных, для каждого из которых задается значение функции на этом наборе. Такой способ хорош, когда число переменных относительно невелико. Уже при n > 5 представление становится плохо обозримым.

Другой способ состоит в том, чтобы задавать функцию некоторой формулой, используя известные достаточно простые функции. Система функций {f 1 , f 2 , … f k } называется полной, если любую логическую функцию можно выразить формулой, содержащей только функции f i .

Полной является система функций {¬, ˄, ˅}. Законы 9 и 10 являются примерами, демонстрирующими, как импликация и тождество выражается через отрицание, конъюнкцию и дизъюнкцию.

Фактически полной является и система из двух функций – отрицания и конъюнкции или отрицания и дизъюнкции. Из законов де-Моргана следуют представления, позволяющие выразить конъюнкцию через отрицание и дизъюнкцию и соответственно выразить дизъюнкцию через отрицание и конъюнкцию:

(а ˅ b) ≡ ¬(¬а ˄ ¬b)
(а ˄ b) ≡ ¬(¬а ˅ ¬b)

Парадоксально, но полной является система, состоящая всего из одной функции. Существуют две бинарные функции – антиконънкция и антидизъюнкция, называемые стрелкой Пирса и штрих Шеффера, представляющие полую систему.

В состав базовых функций языков программирования включают обычно тождество, отрицание, конъюнкцию и дизъюнкцию. В задачах ЕГЭ наряду с этими функциями часто встречается импликация.

Рассмотрим несколько простых задач, связанных с логическими функциями.

Задача 15:

Дан фрагмент таблицы истинности. Какая из трех приведенных функций соответствует этому фрагменту?

X 1	X 2	X 3	X 4	F
1	1	0	0	1
0	1	1	1	1
1	0	0	1	0

(X 1 → X 2) ˄ ¬ X 3 ˅ X 4
(¬ X 1 ˄ X 2) ˅ (¬X 3 ˄ X 4)
¬ X 1 ˅ X 2 ˅ (X 3 ˄ X 4)

Функция под номером 3.

Для решения задачи нужно знать таблицы истинности базовых функций и помнить о приоритетах операций. Напомню, что конъюнкция (логическое умножение) имеет более высокий приоритет и выполняется раньше, чем дизъюнкция (логическое сложение). При вычислениях нетрудно заметить, что функции с номерами 1 и 2 на третьем наборе имеют значение 1 и уже по этой причине фрагменту не соответствуют.

Задача 16:

Какое из приведенных чисел удовлетворяет условию:

(цифры, начиная со старшего разряда, идут в порядке убывания) → (число — четное) ˄ (младшая цифра – четная) ˄ (старшая цифра – нечетная)

Если таких чисел несколько, укажите наибольшее.

13579
97531
24678
15386

Условию удовлетворяет число под номером 4.

Первые два числа условию не удовлетворяют уже по той причине, что младшая цифра является нечетной. Конъюнкция условий ложна, если один из членов конъюнкции ложен. Для третьего числа не выполняется условие для старшей цифры. Для четвертого числа выполняются условия, накладываемые на младшую и старшую цифры числа. Первый член конъюнкции также истинен, поскольку импликация истинна, если ее посылка ложна, что имеет место в данном случае.

Задача 17: Два свидетеля дали следующие показания:

Первый свидетель: Если А виновен, то В и подавно виновен, а С – невиновен.

Второй свидетель: Виновны двое. А точно виновен и виновен один из оставшихся, но кто именно сказать не могу.

Какие заключения о виновности А, В и С можно сделать на основании свидетельских показаний?

Ответ: Из свидетельских показаний следует, что А и В виновны, а С – невиновен.

Решение: Конечно, ответ можно дать, основываясь на здравом смысле. Но давайте рассмотрим, как это можно сделать строго и формально.

Первое, что нужно сделать – это формализовать высказывания. Введем три логические переменные — А, В и С, каждая из которых имеет значение true (1), если соответствующий подозреваемый виновен. Тогда показания первого свидетеля задаются формулой:

A → (B ˄ ¬C)

Показания второго свидетеля задаются формулой:

A ˄ ((B ˄ ¬C) ˅ (¬B ˄ C))

Показания обоих свидетелей полагаются истинными и представляют конъюнкцию соответствующих формул.

Построим таблицу истинности для этих показаний:

A	B	C	F 1	F 2	F 1 ˄ F 2
0	0	0	1	0	0
0	0	1	1	0	0
0	1	0	1	0	0
0	1	1	1	0	0
1	0	0	0	0	0
1	0	1	0	1	0
1	1	0	1	1	1
1	1	1	0	0	0

Суммарные свидетельские показания истинны только в одном случае, приводящие к однозначному ответу – А и В виновны, а С – невиновен.

Из анализа этой таблицы также следует, что показания второго свидетеля более информативны. Из истинности его показания следует только два возможных варианта — А и В виновны, а С – невиновен или А и С виновны, а В – невиновен. Показания первого свидетеля менее информативны – существует 5 различных вариантов, соответствующих его показаниям. Совместно показания обоих свидетелей дают однозначный ответ о виновности подозреваемых.

Логические уравнения и системы уравнений

Пусть F(x 1 , x 2 , …x n) – логическая функция от n переменных. Логическое уравнение имеет вид:

F(x 1 , x 2 , …x n) = С,

Константа С имеет значение 1 или 0.

Логическое уравнение может иметь от 0 до 2 n различных решений. Если С равно 1, то решениями являются все те наборы переменных из таблицы истинности, на которых функция F принимает значение истина (1). Оставшиеся наборы являются решениями уравнения при C, равном нулю. Можно всегда рассматривать только уравнения вида:

F(x 1 , x 2 , …x n) = 1

Действительно, пусть задано уравнение:

F(x 1 , x 2 , …x n) = 0

В этом случае можно перейти к эквивалентному уравнению:

¬F(x 1 , x 2 , …x n) = 1

Рассмотрим систему из k логических уравнений:

F 1 (x 1 , x 2 , …x n) = 1

F 2 (x 1 , x 2 , …x n) = 1

F k (x 1 , x 2 , …x n) = 1

Решением системы является набор переменных, на котором выполняются все уравнения системы. В терминах логических функций для получения решения системы логических уравнений следует найти набор, на котором истинна логическая функция Ф, представляющая конъюнкцию исходных функций F:

Ф = F 1 ˄ F 2 ˄ … F k

Если число переменных невелико, например, менее 5, то нетрудно построить таблицу истинности для функции Ф, что позволяет сказать, сколько решений имеет система и каковы наборы, дающие решения.

В некоторых задачах ЕГЭ по нахождению решений системы логических уравнений число переменных доходит до значения 10. Тогда построить таблицу истинности становится практически неразрешимой задачей. Для решения задачи требуется другой подход. Для произвольной системы уравнений не существует общего способа, отличного от перебора, позволяющего решать такие задачи.

В предлагаемых на экзамене задачах решение обычно основано на учете специфики системы уравнений. Повторяю, кроме перебора всех вариантов набора переменных, общего способа решения задачи нет. Решение нужно строить исходя из специфики системы. Часто полезно провести предварительное упрощение системы уравнений, используя известные законы логики. Другой полезный прием решения этой задачи состоит в следующем. Нам интересны не все наборы, а только те, на которых функция Ф имеет значение 1. Вместо построения полной таблицы истинности будем строить ее аналог — бинарное дерево решений. Каждая ветвь этого дерева соответствует одному решению и задает набор, на котором функция Ф имеет значение 1. Число ветвей в дереве решений совпадает с числом решений системы уравнений.

Что такое бинарное дерево решений и как оно строится, поясню на примерах нескольких задач.

Задача 18

Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, которые удовлетворяют системе из двух уравнений?

Ответ: Система имеет 36 различных решений.

Решение: Система уравнений включает два уравнения. Найдем число решений для первого уравнения, зависящего от 5 переменных – x 1 , x 2 , …x 5 . Первое уравнение можно в свою очередь рассматривать как систему из 5 уравнений. Как было показано, система уравнений фактически представляет конъюнкцию логических функций. Справедливо и обратное утверждение, — конъюнкцию условий можно рассматривать как систему уравнений.

Построим дерево решений для импликации (x1→ x2) — первого члена конъюнкции, который можно рассматривать как первое уравнение. Вот как выглядит графическое изображение этого дерева:

Дерево состоит из двух уровней по числу переменных уравнения. Первый уровень описывает первую переменную X 1 . Две ветви этого уровня отражают возможные значения этой переменной – 1 и 0. На втором уровне ветви дерева отражают только те возможные значения переменной X 2 , для которых уравнение принимает значение истина. Поскольку уравнение задает импликацию, то ветвь, на которой X 1 имеет значение 1, требует, чтобы на этой ветви X 2 имело значение 1. Ветвь, на которой X 1 имеет значение 0, порождает две ветви со значениями X 2 , равными 0 и 1. Построенное дерево задает три решения, на которых импликация X 1 → X 2 принимает значение 1. На каждой ветви выписан соответствующий набор значений переменных, дающий решение уравнения.

Вот эти наборы: {(1, 1), (0, 1), (0, 0)}

Продолжим построение дерева решений, добавляя следующее уравнение, следующую импликацию X 2 → X 3 . Специфика нашей системы уравнений в том, что каждое новое уравнение системы использует одну переменную из предыдущего уравнения, добавляя одну новую переменную. Поскольку переменная X 2 уже имеет значения на дереве, то на всех ветвях, где переменная X 2 имеет значение 1, переменная X 3 также будет иметь значение 1. Для таких ветвей построение дерева продолжается на следующий уровень, но новые ветви не появляются. Единственная ветвь, где переменная X 2 имеет значение 0, даст разветвление на две ветви, где переменная X 3 получит значения 0 и 1. Таким образом, каждое добавление нового уравнения, учитывая его специфику, добавляет одно решение. Исходное первое уравнение:

(x1→x2) /\ (x2→x3) /\ (x3→x4) /\ (x4→x5) = 1
имеет 6 решений. Вот как выглядит полное дерево решений для этого уравнения:

Второе уравнение нашей системы аналогично первому:

(y1→y2) /\ (y2→y3) /\ (y3→y4) /\ (y4→y5) = 1

Разница лишь в том, что в уравнении используются переменные Y. Это уравнение также имеет 6 решений. Поскольку каждое решение для переменных X i может быть скомбинировано с каждым решением для переменных Y j , то общее число решений равно 36.

Заметьте, построенное дерево решений дает не только число решений (по числу ветвей), но и сами решения, выписанные на каждой ветви дерева.

Задача 19

Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, которые удовлетворяют всем перечисленным ниже условиям?

(x1→x2) /\ (x2→x3) /\ (x3→x4) /\ (x4→x5) = 1
(y1→y2) /\ (y2→y3) /\ (y3→y4) /\ (y4→y5) = 1
(x1→y1) = 1

Эта задача является модификацией предыдущей задачи. Разница в том, что добавляется еще одно уравнение, связывающее переменные X и Y.

Из уравнения X 1 → Y 1 следует, что когда X 1 имеет значение 1(одно такое решение существует), то и Y 1 имеет значение 1. Таким образом, существует один набор, на котором X 1 и Y 1 имеют значения 1. При X 1 , равном 0, Y 1 может иметь любое значение, как 0, так и 1. Поэтому каждому набору с X 1 , равном 0, а таких наборов 5, соответствует все 6 наборов с переменными Y. Следовательно, общее число решений равно 31.

Задача 20

(¬X 1 ˅ X 2) ˄ (¬X 2 ˅ X 3) ˄ (¬X 3 ˅ X 4) ˄ (¬X 4 ˅ X 5) ˄ (¬X 5 ˅ X 1) = 1

Решение: Вспоминания основные эквивалентности, запишем наше уравнение в виде:

(X 1 → X 2) ˄ (X 2 → X 3) ˄ (X 3 → X 4) ˄ (X 4 → X 5) ˄ (X 5 → X 1) = 1

Циклическая цепочка импликаций означает тождественность переменных, так что наше уравнение эквивалентно уравнению:

X 1 ≡ X 2 ≡ X 3 ≡ X 4 ≡ X 5 = 1

Это уравнение имеет два решения, когда все X i равны либо 1, либо 0.

Задача 21

(X 1 → X 2) ˄ (X 2 → X 3) ˄ (X 3 → X 4) ˄ (X 4 → X 2) ˄ (X 4 → X 5) = 1

Решение: Так же, как и в задаче 20, от циклических импликаций перейдем к тождествам, переписав уравнение в виде:

(X 1 → X 2) ˄ (X 2 ≡ X 3 ≡ X 4) ˄ (X 4 → X 5) = 1

Построим дерево решений для этого уравнения:

Задача 22

Сколько решений имеет следующая система уравнений?

((X 1 ≡ X 2) ˄ (X 3 ≡ X 4)) ˅(¬(X 1 ≡ X 2) ˄ ¬(X 3 ≡ X 4)) = 0

((X 3 ≡ X 4) ˄ (X 5 ≡ X 6)) ˅(¬(X 3 ≡ X 4) ˄ ¬(X 5 ≡ X 6)) = 0

((X 5 ≡ X 6) ˄ (X 7 ≡ X 8)) ˅(¬(X 5 ≡ X 6) ˄ ¬(X 7 ≡ X 8)) = 0

((X 7 ≡ X 8) ˄ (X 9 ≡ X 10)) ˅(¬(X 7 ≡ X 8) ˄ ¬(X 9 ≡ X 10)) = 0

Ответ: 64

Решение: Перейдем от 10 переменных к 5 переменным, введя следующую замену переменных:

Y 1 = (X 1 ≡ X 2); Y 2 = (X 3 ≡ X 4); Y 3 = (X 5 ≡ X 6); Y 4 = (X 7 ≡ X 8); Y 5 = (X 9 ≡ X 10);

Тогда первое уравнение примет вид:

(Y 1 ˄ Y 2) ˅ (¬Y 1 ˄ ¬Y 2) = 0

Уравнение можно упростить, записав его в виде:

(Y 1 ≡ Y 2) = 0

Переходя к традиционной форме, запишем систему после упрощений в виде:

¬(Y 1 ≡ Y 2) = 1

¬(Y 2 ≡ Y 3) = 1

¬(Y 3 ≡ Y 4) = 1

¬(Y 4 ≡ Y 5) = 1

Дерево решений для этой системы простое и состоит из двух ветвей с чередующимися значениями переменных:

Возвращаясь к исходным переменным X, заметим, что каждому значению переменной Y соответствует 2 значения переменных X, поэтому каждое решение в переменных Yпорождает 2 5 решений в переменных X. Две ветви порождают 2 * 2 5 решений, так что общее число решений равно 64.

Как видите, каждая задача на решение системы уравнений требует своего подхода. Общим приемом является выполнение эквивалентных преобразований для упрощения уравнений. Общим приемом является и построение деревьев решений. Применяемый подход частично напоминает построение таблицы истинности с той особенностью, что строятся не все наборы возможных значений переменных, а лишь те, на которых функция принимает значение 1 (истина). Часто в предлагаемых задачах нет необходимости в построении полного дерева решений, поскольку уже на начальном этапе удается установить закономерность появления новых ветвей на каждом следующем уровне, как это сделано, например, в задаче 18.

В целом задачи на нахождение решений системы логических уравнений являются хорошими математическими упражнениями.

Если задачу трудно решить вручную, то можно поручить решение задачи компьютеру, написав соответствующую программу решения уравнений и систем уравнений.

Написать такую программу несложно. Такая программа легко справится со всеми задачами, предлагаемыми в ЕГЭ.

Как это ни странно, но задача нахождения решений систем логических уравнений является сложной и для компьютера, оказывается и у компьютера есть свои пределы. Компьютер может достаточно просто справиться с задачами, где число переменных 20 -30, но начнет надолго задумываться на задачах большего размера. Дело в том, что функция 2 n , задающая число наборов, является экспонентой, быстро растущей с увеличением n. Настолько быстро, что обычный персональный компьютер за сутки не справится с задачей, у которой 40 переменных.

Программа на языке C# для решения логических уравнений

Написать программу для решения логических уравнений полезно по многим причинам, хотя бы потому, что с ее помощью можно проверять правильность собственного решения тестовых задач ЕГЭ. Другая причина в том, что такая программа является прекрасным примером задачи на программирование, соответствующей требованиям, предъявляемым к задачам категории С в ЕГЭ.

Идея построения программы проста, — она основана на полном переборе всех возможных наборов значений переменных. Поскольку для заданного логического уравнения или системы уравнений число переменных n известно, то известно и число наборов – 2 n , которые требуется перебрать. Используя базовые функции языка C# — отрицание, дизъюнкцию, конъюнкцию и тождество, нетрудно написать программу, которая для заданного набора переменных вычисляет значение логической функции, соответствующей логическому уравнению или системе уравнений.

В такой программе нужно построить цикл по числу наборов, в теле цикла по номеру набора сформировать сам набор, вычислить значение функции на этом наборе, и если это значение равно 1, то набор дает решение уравнения.

Единственная сложность, возникающая при реализации программы, связана с задачей формирования по номеру набора самого набора значений переменных. Красота этой задачи в том, что эта, казалось бы, трудная задача, фактически сводится к простой, уже неоднократно возникавшей задаче. Действительно, достаточно понять, что соответствующий числу i набор значений переменных, состоящий из нулей и единиц, представляет двоичную запись числа i. Так что сложная задача получения набора значений переменных по номеру набора сводится к хорошо знакомой задаче перевода числа в двоичную систему.

Вот как выглядит функция на языке C#, решающая нашу задачу:

///

/// программа подсчета числа решений

/// логического уравнения (системы уравнений)

///

/// логическая функция — метод,

/// сигнатура которого задается делегатом DF

///

/// число переменных

/// число решений

static int SolveEquations(DF fun, int n)

bool set = new bool[n];

int m = (int)Math.Pow(2, n); //число наборов

int p = 0, q = 0, k = 0;

//Полный перебор по числу наборов

for (int i = 0; i < m; i++)

//Формирование очередного набора — set,

//заданного двоичным представлением числа i

for (int j = 0; j < n; j++)

k = (int)Math.Pow(2, j);

//Вычисление значения функции на наборе set

Для понимания программы, надеюсь, достаточно сделанных объяснений идеи программы и комментариев в ее тексте. Остановлюсь лишь на пояснении заголовка приведенной функции. У функции SolveEquations два входных параметра. Параметр fun задает логическую функцию, соответствующую решаемому уравнению или системе уравнений. Параметр n задает число переменных функции fun. В качестве результата функция SolveEquations возвращает число решений логической функции, то есть число тех наборов, на которых функция принимает значение true.

Для школьников привычно, когда у некоторой функции F(x) входным параметром x является переменная арифметического, строкового или логического типа. В нашем случае используется более мощная конструкция. Функция SolveEquations относится к функциям высшего порядка – функциям типа F(f), у которых параметрами могут быть не только простые переменные, но и функции.

Класс функций, которые могут передаваться в качестве параметра функции SolveEquations, задается следующим образом:

delegate bool DF(bool vars);

Этому классу принадлежат все функции, которым в качестве параметра передается набор значений логических переменных, заданных массивом vars. В качестве результата возвращается значение булевского типа, представляющее значение функции на этом наборе.

В заключение приведу программу, в которой функция SolveEquations используется для решения нескольких систем логических уравнений. Функция SolveEquations является частью приводимого ниже класса ProgramCommon:

class ProgramCommon

delegate bool DF(bool vars);

static void Main(string args)

Console.WriteLine(«У Функции And решений — » +

SolveEquations(FunAnd, 2));

Console.WriteLine(«У Функции 51 решений — » +

SolveEquations(Fun51, 5));

Console.WriteLine(«У Функции 53 решений — » +

SolveEquations(Fun53, 10));

static bool FunAnd(bool vars)

return vars && vars;

static bool Fun51(bool vars)

f = f && (!vars || vars);

static bool Fun53(bool vars)

f = f && ((vars == vars) || (vars == vars));

f = f && (!((vars == vars) || (vars == vars)));

Вот как выглядят результаты решения по этой программе:

10 задач для самостоятельной работы

Какие из трех функций эквивалентны:
1. (X → Y) ˅ ¬Y
2. ¬(X ˅ ¬Y) ˄ (X → ¬Y)
3. ¬X ˄ Y
Дан фрагмент таблицы истинности:

X 1	X 2	X 3	X 4	F
1	0	0	1	1
0	1	1	1	1
1	0	1	0	0

Какой из трех функций соответствует этот фрагмент:

(X 1 ˅ ¬X 2) ˄ (X 3 → X 4)
(X 1 → X 3) ˄ X 2 ˅ X 4
X 1 ˄ X 2 ˅ (X 3 → (X 1 ˅ X 4))
В состав жюри входят три человека. Решение принимается, если за него голосует председатель жюри, поддержанный хотя бы одним из членов жюри. В противном случае решение не принимается. Постройте логическую функцию, формализующую процесс принятия решения.
X выигрывает у Y, если при четырех бросаниях монеты трижды выпадает «орёл». Задайте логическую функцию, описывающую выигрыш X.
Слова в предложении нумеруются, начиная с единицы. Предложение считается правильно построенным, если выполняются следующие правила:
1. Если четное в нумерации слово заканчивается на гласную, то следующее слово, если оно существует, должно начинаться с гласной.
2. Если нечетное в нумерации слово заканчивается согласной, то следующее слово, если оно существует, должно начинаться с согласной и заканчиваться гласной.
  Какие из следующих предложений правильно построены:
3. Мама мыла Машу мылом.
4. Лидер всегда является образцом.
5. Правда хорошо, а счастье лучше.
Сколько решений имеет уравнение:
(a ˄ ¬ b) ˅ (¬a ˄ b) → (c ˄ d) = 1
Перечислите все решения уравнения:
(a → b) → c = 0
Сколько решений имеет следующая система уравнений:
X 0 → X 1 ˄ X 1 → X 2 = 1
X 2 → X 3 ˄ X 3 → X 4 = 1
X 5 → X 6 ˄ X 6 → X 7 = 1
X 7 → X 8 ˄ X 8 → X 9 = 1
X 0 → X 5 = 1
Сколько решений имеет уравнение:
((((X 0 → X 1) → X 2) → X 3) →X 4) →X 5 = 1

Ответы к задачам:

Эквивалентными являются функции b и c.
Фрагмент соответствует функции b.
Пусть логическая переменная P принимает значение 1, когда председатель жюри голосует «за» принятие решения. Переменные M 1 и M 2 представляют мнение членов жюри. Логическая функция, задающая принятие положительного решения может быть записана так:
P ˄ (M 1 ˅ M 2)
Пусть логическая переменная P i принимает значение 1, когда при i-м бросании монеты выпадает «орёл». Логическая функция, задающая выигрыш X может быть записана так:
¬((¬P 1 ˄ (¬P 2 ˅ ¬P 3 ˅ ¬P 4)) ˅
(¬P 2 ˄ (¬P 3 ˅ ¬P 4)) ˅
(¬P 3 ˄ ¬P 4))
Предложение b.
Уравнение имеет 3 решения: (a = 1; b = 1; c = 0); (a = 0; b = 0; c = 0); (a = 0; b = 1; c = 0)

Пусть – логическая функция от n переменных. Логическое уравнение имеет вид:

Константа С имеет значение 1 или 0.

Логическое уравнение может иметь от 0 до различных решений. Если С равно 1, то решениями являются все те наборы переменных из таблицы истинности, на которых функция F принимает значение истина (1). Оставшиеся наборы являются решениями уравнения при C, равном нулю. Можно всегда рассматривать только уравнения вида:

Действительно, пусть задано уравнение:

В этом случае можно перейти к эквивалентному уравнению:

Рассмотрим систему из k логических уравнений:

Если число переменных невелико, например, менее 5, то нетрудно построить таблицу истинности для функции , что позволяет сказать, сколько решений имеет система и каковы наборы, дающие решения.

В предлагаемых на экзамене задачах решение обычно основано на учете специфики системы уравнений. Повторяю, кроме перебора всех вариантов набора переменных, общего способа решения задачи нет. Решение нужно строить исходя из специфики системы. Часто полезно провести предварительное упрощение системы уравнений, используя известные законы логики. Другой полезный прием решения этой задачи состоит в следующем. Нам интересны не все наборы, а только те, на которых функция имеет значение 1. Вместо построения полной таблицы истинности будем строить ее аналог - бинарное дерево решений. Каждая ветвь этого дерева соответствует одному решению и задает набор, на котором функция имеет значение 1. Число ветвей в дереве решений совпадает с числом решений системы уравнений.

Что такое бинарное дерево решений и как оно строится, поясню на примерах нескольких задач.

Задача 18

Ответ: Система имеет 36 различных решений.

Решение: Система уравнений включает два уравнения. Найдем число решений для первого уравнения, зависящего от 5 переменных – . Первое уравнение можно в свою очередь рассматривать как систему из 5 уравнений. Как было показано, система уравнений фактически представляет конъюнкцию логических функций. Справедливо и обратное утверждение, - конъюнкцию условий можно рассматривать как систему уравнений.

Построим дерево решений для импликации () - первого члена конъюнкции, который можно рассматривать как первое уравнение. Вот как выглядит графическое изображение этого дерева

Дерево состоит из двух уровней по числу переменных уравнения. Первый уровень описывает первую переменную . Две ветви этого уровня отражают возможные значения этой переменной – 1 и 0. На втором уровне ветви дерева отражают только те возможные значения переменной , для которых уравнение принимает значение истина. Поскольку уравнение задает импликацию, то ветвь, на которой имеет значение 1, требует, чтобы на этой ветви имело значение 1. Ветвь, на которой имеет значение 0, порождает две ветви со значениями , равными 0 и 1. Построенное дерево задает три решения, на которых импликация принимает значение 1. На каждой ветви выписан соответствующий набор значений переменных, дающий решение уравнения.

Вот эти наборы: {(1, 1), (0, 1), (0, 0)}

Продолжим построение дерева решений, добавляя следующее уравнение, следующую импликацию . Специфика нашей системы уравнений в том, что каждое новое уравнение системы использует одну переменную из предыдущего уравнения, добавляя одну новую переменную. Поскольку переменная уже имеет значения на дереве, то на всех ветвях, где переменная имеет значение 1, переменная также будет иметь значение 1. Для таких ветвей построение дерева продолжается на следующий уровень, но новые ветви не появляются. Единственная ветвь, где переменная имеет значение 0, даст разветвление на две ветви, где переменная получит значения 0 и 1. Таким образом, каждое добавление нового уравнения, учитывая его специфику, добавляет одно решение. Исходное первое уравнение:

имеет 6 решений. Вот как выглядит полное дерево решений для этого уравнения:

Второе уравнение нашей системы аналогично первому:

Разница лишь в том, что в уравнении используются переменные Y. Это уравнение также имеет 6 решений. Поскольку каждое решение для переменных может быть скомбинировано с каждым решением для переменных , то общее число решений равно 36.